Topic Modeling Methodologies

Introduction

1. Probabilistic Latent Semantic Analysis (pLSA): pLSA is a precursor to LDA and is based on a generative probabilistic model. It discovers latent topics in a document collection by modeling the co-occurrence of words and documents as a mixture of multinomial distributions. Despite its success in revealing hidden topics, pLSA suffers from overfitting due to the lack of regularization.

2. Latent Dirichlet Allocation (LDA): LDA is a widely-used generative probabilistic model for topic modeling, which extends pLSA by incorporating Dirichlet priors for document-topic and topic-term distributions. LDA’s assumptions about the generative process of documents and the incorporation of Dirichlet priors help in overcoming overfitting and provide better generalization.

3. Non-negative Matrix Factorization (NMF): NMF is a linear algebraic method for dimensionality reduction, which has been applied to topic modeling. NMF factorizes the document-term matrix into two non-negative lower-dimensional matrices representing document-topic and topic-term relationships. Although NMF lacks the probabilistic foundation of LDA, it often results in more interpretable topics.

4. Correlated Topic Model (CTM): CTM is an extension of LDA that allows topics to be correlated, capturing more complex relationships between topics. In CTM, the distribution of topics within documents is modeled using a logistic normal distribution instead of a Dirichlet distribution. This approach results in more realistic topic models, especially when topics are not independent in the underlying data.

5. Dynamic Topic Models (DTM): DTM is a class of topic models designed to analyze the evolution of topics over time. By modeling topic distributions as a function of time, DTMs can capture the temporal dynamics of topics in ordered document collections. This makes DTMs suitable for analyzing text data with an inherent temporal structure, such as news articles or scientific publications.

Each of these topic modeling methodologies offers unique advantages and drawbacks, catering to different needs and data types. By understanding the underlying principles and assumptions of these methods, researchers and practitioners can select the most appropriate approach for their specific text data analysis tasks and effectively extract meaningful insights from large-scale unstructured document collections.

Probabilistic Latent Semantic Analysis (pLSA)

Probabilistic Latent Semantic Analysis (pLSA) is a topic modeling technique that aims to uncover latent topics within a collection of documents by utilizing a generative probabilistic model. Introduced by Thomas Hofmann in 1999, pLSA is a precursor to the more popular Latent Dirichlet Allocation (LDA). It models the co-occurrence of words and documents as a mixture of multinomial distributions, attempting to capture the hidden structure that governs these co-occurrences.

In pLSA, each document is considered a mixture of topics, and each topic is represented as a distribution over words. The underlying assumption is that the observed words in a document are generated by first selecting a topic and then sampling a word from the corresponding word distribution of the selected topic. The goal of pLSA is to learn these latent topic distributions and the document-topic relationships that best explain the observed data.

The pLSA model is trained using the Expectation-Maximization (EM) algorithm, which iteratively refines the estimates of topic distributions and document-topic relationships. During the Expectation step, the algorithm computes the posterior probabilities of topics given the words and the current model parameters. In the Maximization step, the model parameters are updated to maximize the likelihood of the observed data given these posterior probabilities.

While pLSA has been successful in revealing latent topics in text data, it has some limitations:

1. Overfitting: pLSA is prone to overfitting due to the lack of regularization or priors in the model. This can result in poor generalization to new, unseen documents.

2. Parameter growth: The number of parameters in pLSA grows linearly with the number of documents, making it computationally expensive for large-scale document collections.

3. No generative model for new documents: pLSA does not provide an explicit generative model for creating topic distributions for new documents, which makes it difficult to apply the learned model to new data.

Despite these limitations, pLSA laid the foundation for more advanced topic modeling techniques, such as Latent Dirichlet Allocation (LDA), which incorporates Dirichlet priors to address the overfitting issue and provides a more comprehensive generative model for document collections.

Latent Dirichlet Allocation (LDA)

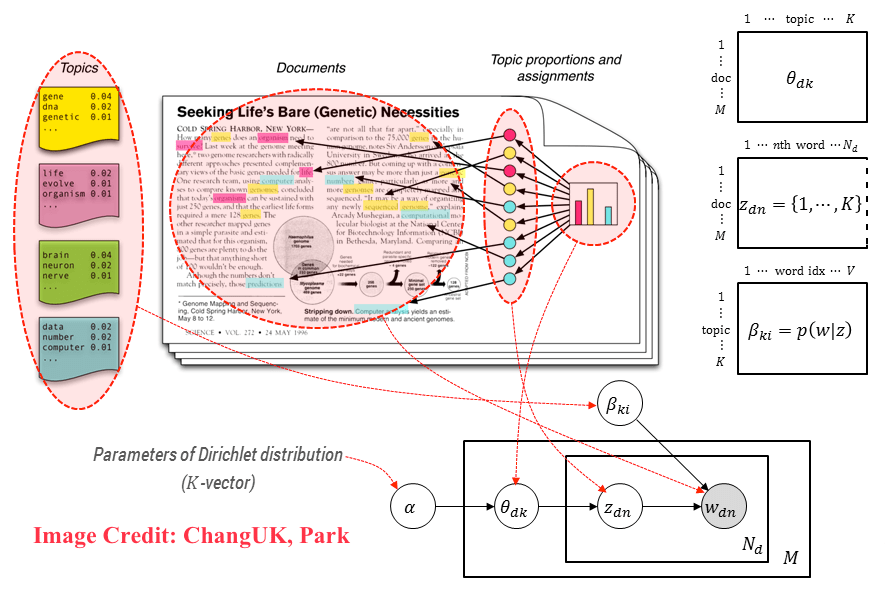
Fig. 41 Latent Dirichlet Allocation

Latent Dirichlet Allocation (LDA) is a popular generative probabilistic model used for topic modeling. As the name suggests, it involves discovering hidden (latent) topics within a collection of documents, where Dirichlet refers to the type of probability distribution used for modeling. LDA assumes that each document is a mixture of topics, and each topic is a distribution over words. The main goal is to find these hidden topic distributions and their relationships to the documents.

In LDA, given an \(N \times M\) document-term count matrix \(X\), where \(N\) represents the number of documents and \(M\) denotes the number of unique terms or words in the corpus, we assume there are \(K\) topics to be discovered. The number of topics, \(K\), is a tunable hyperparameter, and its optimal value can be found using methods like coherence score analysis.

LDA, similar to PCA and NMF, aims to factorize the document-term matrix \(X\) into two lower-dimensional matrices:

1. An \(N \times K\) document-topic matrix: This matrix represents the relationship between documents and topics, with each element indicating the contribution of a particular topic to a specific document.

2. A \(K \times M\) topic-term matrix: This matrix represents the relationship between topics and terms, with each element denoting the probability of a word belonging to a specific topic.

LDA operates under the assumption that documents are generated through the following process:

1. For each document, choose a distribution over topics.

2. For each word in the document: a. Choose a topic according to the document’s distribution over topics. b. Choose a word from the topic’s distribution over words.

By applying LDA, we can infer the hidden topic structure of the documents, making it easier to understand, navigate, and analyze large-scale unstructured text data. LDA has been widely used for various applications, including document clustering, text summarization, and information retrieval, among others.

Fig. 42 LDA Example

When applying Latent Dirichlet Allocation (LDA) to a set of questions, the goal is to discover the hidden topic structure that characterizes these questions. For instance, consider the following four questions:

1. How do football players stay safe?

2. What is the most hated NFL football team of all time?

3. Who is the greatest political leader in the world and why?

4. Why do people treat politics like it’s a football team or some kind of sport?

Fitting LDA to these questions would result in topic assignments that might look like the following:

• Question 1: 100% Topic A

• Question 2: 90% Topic A, 10% Topic C

• Question 3: 100% Topic B

• Question 4: 40% Topic A, 60% Topic B

In this example, Topic A appears to be related to sports, while Topic B is associated with politics, and Topic C might represent a more specific aspect of football, such as team rivalries or sentiments.

Using these topic assignments, we can then infer the topics for each original question:

1. How do football players stay safe? (Sport)

2. What is the most hated NFL football team of all time? (Sport, with a small contribution from team rivalries or sentiments)

3. Who is the greatest political leader in the world and why? (Politics)

4. Why do people treat politics like it’s a football team or some kind of sport? (Sport, Politics)

Fig. 43 LDA Example Topics

LDA represents each question as a probability distribution of topics and each topic as a probability distribution of words. In other words, every question can be seen as a mixture of topics, and every topic can be viewed as a mixture of words.

Fig. 44 LDA Example Topic Distribution

When fitting LDA to a collection of questions or documents, the algorithm attempts to find the best topic mix and word mix that explain the observed data. This process uncovers the latent topic structure in the data, providing valuable insights into the thematic relationships between questions or documents and facilitating more efficient text data exploration and analysis.

Non-negative Matrix Factorization (NMF)

Fig. 45 Non-negative Matrix Factorization

Non-negative Matrix Factorization (NMF) is a linear algebraic method used for dimensionality reduction and data representation. It has been widely applied in various fields, including image processing, signal processing, and text mining, where it has been utilized for topic modeling. NMF was introduced by Lee and Seung in 1999 as a method to decompose a non-negative data matrix into two non-negative lower-dimensional matrices that, when multiplied, approximate the original data matrix.

Given a non-negative document-term matrix \(X\) of size \(N \times M\), where \(N\) is the number of documents and \(M\) is the number of unique terms in the corpus, NMF aims to find two non-negative matrices \(W\) and \(H\) such that \(X \approx WH\), where \(W\) is an \(N \times K\) document-topic matrix and \(H\) is a \(K \times M\) topic-term matrix. Here, \(K\) is the number of topics or latent factors.

The primary objective of NMF is to minimize the reconstruction error between the original matrix \(X\) and its approximation \(WH\). This is achieved by iteratively updating the elements of \(W\) and \(H\) using multiplicative update rules or other optimization algorithms, such as gradient descent or alternating least squares.

Consider the following three questions:

1. How do football players stay safe?

2. What is the most hated NFL football team of all time?

3. Who is the greatest political leader in the world and why?

To apply Non-negative Matrix Factorization (NMF) for topic modeling on these questions, we first create a term-document matrix that represents the frequency of terms in each question. This matrix will have rows representing unique terms and columns representing the questions.

Next, we choose the number of topics, k=2 in this case, and decompose the term-document matrix into two non-negative matrices: a term-topic matrix (n words by k topics) and a document-topic matrix (k topics by m original documents).

The term-topic matrix represents the relationship between terms and topics, where each topic is characterized by a distribution of words. The document-topic matrix represents the relationship between documents (questions) and topics, where each document is a mixture of topics with varying proportions.

Fig. 46 Non-negative Matrix Factorization Example

After applying NMF, we can examine the resulting term-topic and document-topic matrices to identify the underlying topics and their association with the original questions. For instance, we might find that Topic 1 is related to football and sports, while Topic 2 is related to politics and leadership. The document-topic matrix would then show the extent to which each question is associated with these topics, allowing us to interpret the hidden topic structure in the data.

Fig. 47 Non-negative Matrix Factorization Example Result

NMF has several attractive properties that make it suitable for topic modeling:

1. Non-negativity constraint: The non-negativity constraint on the factor matrices ensures that the resulting topics and their relationships to documents are interpretable, as they reflect additive combinations of the original features.

2. Sparsity: NMF often results in sparse representations, where each document is associated with only a few topics, and each topic is characterized by a limited set of words. This sparsity promotes interpretability and simplifies the identification of meaningful topics.

3. Flexibility: NMF can be adapted to different problem settings by incorporating additional constraints or using different objective functions, such as the Kullback-Leibler divergence or the Itakura-Saito divergence, to better capture the underlying structure of the data.

However, NMF also has some limitations:

1. Lack of probabilistic foundation: Unlike LDA, NMF is not based on a probabilistic generative model, which may limit its applicability in certain scenarios where probabilistic interpretations are desired.

2. Non-unique solutions: NMF does not guarantee unique factorization, as there can be multiple combinations of \(W\) and \(H\) that approximate the original matrix \(X\). This can lead to inconsistencies in the extracted topics.

Despite these limitations, NMF remains a popular and useful technique for topic modeling, as it often provides interpretable and meaningful topic representations in a computationally efficient manner.

Correlated Topic Model (CTM)

The Correlated Topic Model (CTM) is an extension of the Latent Dirichlet Allocation (LDA) model that takes into account the correlations between topics. CTM, like LDA, is a generative probabilistic model used to discover latent topics in a document collection. However, unlike LDA, which assumes that the topics are independent, CTM allows for modeling correlations between topics, making it better suited for capturing more complex topic structures in the documents.

Overview

In LDA, the topic distribution of each document is generated from a Dirichlet distribution with a fixed concentration parameter. This assumption leads to the independence of topics in the LDA model. On the other hand, CTM assumes that the topic proportions for a document are generated from a logistic normal distribution, which allows for modeling the correlations between topics.

The generative process of CTM can be described as follows:

1. For each topic \(k\), choose a distribution over words \(\beta_k\) from a Dirichlet distribution with parameter \(\eta\).

2. For each document \(d\) in the corpus:

   • a. Choose a topic distribution \(\theta_d\) from a logistic normal distribution with mean \(\mu\) and covariance matrix \(\Sigma\).

   • b. For each word \(w\) in document \(d\):

     • i. Choose a topic \(z_{d,w}\) from the distribution \(\theta_d\).

     • ii. Choose a word \(w_{d,n}\) from the distribution over words for the chosen topic \(\beta_{z_{d,w}}\).

Inference

Inference in CTM is more challenging than in LDA due to the use of the logistic normal distribution. Approximate inference methods, such as variational inference or Markov Chain Monte Carlo (MCMC) sampling, are often employed to estimate the model parameters.

Variational inference for CTM involves optimizing a lower bound on the log likelihood of the observed data using mean-field variational methods. This approach approximates the true posterior distribution with a simpler distribution that can be optimized iteratively to fit the data.

Applications

Like LDA, CTM can be used in various text mining and natural language processing tasks, such as:

• Topic modeling: Discovering the underlying topics in a document collection.

• Document classification: Assigning documents to categories based on their topic distribution.

• Information retrieval: Improving search results by considering topic correlations.

• Recommender systems: Recommending content based on topic similarity.

CTM is particularly useful when there is a need to model complex relationships between topics, which can lead to more accurate and informative topic representations in the documents.

Dynamic Topic Models (DTM)

Dynamic Topic Models (DTM) are an extension of traditional topic models like Latent Dirichlet Allocation (LDA) that incorporate a temporal aspect. The main idea behind DTM is to model how topics evolve over time in a document collection. This allows for the discovery of not only the latent topics but also how their word distributions and prevalence change across different time periods.

Overview

DTM builds on the foundation of LDA by introducing a time component to the generative process. In DTM, the documents are divided into time slices, and a separate LDA model is generated for each time slice. The topics from adjacent time slices are connected through a state-space model, which captures the evolution of topics over time.

The generative process of DTM can be described as follows:

1. For each time slice \(t\):

   • a. For each topic \(k\), choose a distribution over words \(\beta_{t,k}\) from a Dirichlet distribution with parameter \(\eta\).

   • b. For each document \(d\) in time slice \(t\):

     • i. Choose a topic distribution \(\theta_{t,d}\) from a Dirichlet distribution with parameter \(α\).

     • ii. For each word \(w\) in document \(d\):

       1. Choose a topic \(z_{t,d,w}\) from the distribution \(\theta_{t,d}\).

       2. Choose a word \(w_{t,d,n}\) from the distribution over words for the chosen topic \(\beta_{t,z_{t,d,w}}\).

The main difference between DTM and LDA lies in the choice of \(\beta_{t,k}\), which models the evolution of topics across time slices. In DTM, the distribution over words for a topic at time \(t\) is influenced by the distribution over words for the same topic at time \(t-1\).

Inference

Inference in DTM is more challenging than in LDA due to the temporal dependencies between topics across different time slices. Approximate inference methods, such as variational inference or Markov Chain Monte Carlo (MCMC) sampling, are employed to estimate the model parameters. In particular, a specialized variational inference algorithm, called the Kalman variational inference, has been developed for DTM, which takes advantage of the state-space model structure to improve inference efficiency.

Applications

DTM can be applied to various text mining and natural language processing tasks that require the analysis of temporal patterns in documents, such as:

• Temporal topic modeling: Discovering the latent topics and their evolution over time in a document collection.

• Trend analysis: Identifying emerging or declining trends in a corpus.

• Document classification: Assigning documents to categories based on their topic distribution and time information.

• Information retrieval: Improving search results by considering both topic similarity and temporal relevance.

DTM is especially useful when analyzing document collections with a strong temporal component, such as news articles, scientific publications, or social media data, where understanding the dynamics of topics is crucial for accurate analysis and interpretation.